Why You Need Mental Arithmetic

There’s an argument in favor of teaching basic computational skills that starts something line this: The reason you need to be able to do arithmetic hand is that if your calculator ever breaks down…

If you ever hear a math teacher try to defend basic arithmetic facility on this basis, stop them right there and ask them if they know how to process coffee beans, dress a rabbit, smelt iron, and weave cloth.

Because that’s what the “if your calculator breaks down” argument comes down to. If civilization ever collapses, it’s important to know how to do arithmetic by hand. No question about that…but if we base our educational system on what we’d need if civilization collapses, perhaps we’d be better off teaching how to make a fire, grow wheat, or forge metal.

So why do we need to teach arithmetic? There are two reasons. The commonly given reason is that it prepares students for algebra. This is only partially true: done properly, learning arithmetic does prepare students for algebra. Unfortunately, what gets taught as arithmetic generally doesn’t do that. (Here’s the test: if you see no fundamental difference between and minus , you were probably taught arithmetic correctly. If you see the two problems as different, you weren’t)

I’ve advanced this reason in my own classes, so you can take it as given that I believe it’s essentially valid.

But…it begs the question. Why should students learn algebra? The answer is that it’s a stepping stone to calculus, and that’s a requirement if you’re going into a STEM career.

This leads to an ongoing argument about this, based around the incontrovertible fact that most people don’t use algebra.

My response, rendered as a repostable meme:

And that’s the problem. As I see it, the fact that most people don’t use algebra doesn’t mean that algebra isn’t important. It means that we need to encourage its use among those in nonSTEM fields.

But why? Let’s go back to arithmetic. Anyone can calculate with technology. But it takes initiative to break out the piece of technology, so most people don’t bother. This means they take numbers and accept or reject them on the basis of what they believe is true about the world: whether it’s that millions of illegal immigrants vote in elections, or that a Wakandan prince wants to get 25 million in gold out of his country.

What we need, as a society, are citizens who calculate as readily and naturally as they breathe. What that doesn’t require is the ability to do arithmetic by hand.

What it does require is the ability to do arithmetic mentally. The reason is this: if you need a device to perform arithmetic, be it a calculator or pencil and paper, computing requires an extra step beyond the computation: it requires taking out the device and setting it up. As a result, 9 times out of 10, you won’t do it.

On the other hand, if you see and think to yourself, “Self, I I could do that in my head…”, then you’re much more likely to hear “Millions of illegal votes” and think “That means that a bunch of the people in the polling line with me weren’t legally registered…”

(Oh, and if you want to do in your head, here’s how:  is two cents less than eight bucks, so figure:  , minus two cents is .  I’ll do more about common core arithmetic later)

 

The Oldest Computer Program

I’m preparing for my classes next semester, and one of the courses I’ll be teaching is cryptography (a majors-level course).  Perhaps the most remarkable feature about cryptography, and a telling feature about mathematics in general, is the following:

Computer security relies on mathematical algorithms that are at least 250 years old.

Put another way:  250 years ago, there was no practical use for a very broad area of mathematics.  Today, that area of mathematics is the basis of civilization in the 21st century.  Any time you visit a website with an  https designation, you are using a method of encryption that could have been invented by Thomas Jefferson.

A crucial component of modern cryptographic implementations is the fast powering algorithm.  The first recorded appearance of this algorithm was in the work of Pingala, an Indian mathematician who lived in the 3rd century BC.  Pingala not only wrote down the algorithm, but (in modern terms) wrote down a computer program to implement it.  Incidentally, the treatise of Pingala was the first to use the zero symbol (though in Pingala’s manuscript, it’s just a symbol that has no specific meaning).

Here’s a video I’ve prepared on the subject:

Apportionment

It’s election day, and tomorrow there’s going to be a lot of complaints about the results, with good reason: there are many problems with American style democracy, ranging from the electoral college, to gerrymandering, to the presence of big money in politics, to the effective non-existence of third-party candidates.  I’ll talk about those later.

This time, I’ll be more positive and point to one thing we get right in this country, and that’s apportionment.  (And in a later post, I’ll talk about how we can use this to remedy many of the problems above)

Every 10 years, we have a census, and on the basis of those numbers, each state gets a certain number of Congresscritters. The problem of apportionment is deciding how many.

One problem is that we have, for rather stupid reasons, decided there will be exactly 435 Congresscritters. That causes problems I’ll talk about later, but for now we’ll take it as a starting point.

Any such limit necessarily requires us to proceed as follows. First, make an initial assignment. Then fiddle with the numbers until you’ve apportioned the correct numbers.  For illustrative purposes, suppose you have two states, one with a population of 4000 and the other with a population of 16000.  Since there are 4000 + 16000 = 20,000 persons all together, then state 1 should receive 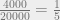of the delegates, and state 2 should receive 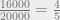of the delegates.

That works…if the number of representatives is divisible by 5.  But what if it isn’t?  Then we might try to get as close as possible to the ideal ratio of for state 1 and for state 2. For example, suppose we have 8 representatives.  We could begin give the first state 2 representatives and the second state 6.

That’s just common sense.  The problem is that common sense doesn’t solve problems: it merely repeats a solution to a different problem.  It’s great if the two problems are the same…not so great if the two problems are fundamentally different.  In this case, the residents of the second state might object:  Even though they have four times the population, they only have three times as many representatives.  Surely this is unfair.

Common sense can’t resolve this issue.  But mathematics can.  We’ll adopt the following strategy:

• Begin with some initial apportionment, leaving some number of representative to be assigned to the states.
• Assign priority values to each of the states, which measure which state is “most deserving” of a representative.
• Give that state an additional representative.
• Recompute the priority values, and give out the next representative.
• Repeat until all representatives have been given out.

Again, suppose we only have two states with populations A and B.  We’ll need to make an initial assignment.  Rather than try and figure out what that initial assignment is (which will, in effect, require us to solve the apportionment problem!), we’ll start each state with its mandated one representative.

Now, we need to choose on a method for deciding which state deserves the next representative.  Since, in theory, our Congresscritters are supposed to represent the people in their districts, then it seems we’ll want to base our decision on how representative they are.

To that end, consider three comparisons:

• and 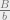, the persons per representative in each of the two states.
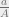• and , the representatives per person in each of the two states.
• and 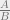, the ratio of the size of the congressional delegations and the ratio of the populations.

In general, these won’t be equal. But this means we can frame the apportionment problem mathematically: assign the next representative in such a way as to reduce the inequality.

Here’s the general approach:  First, choose one of the comparisons.  For example, we might take the first (which corresponds to the size of the congressional districts in each of the two states).  We’ll give each state one representative, then assign the remaining six by determining which state is “more deserving,” based on the goal of trying to make the congressional district sizes equal.

For example, consider our states above, with 4000 and 16,000 people, respectively.  If we start each state with 1 representative, we can assign the next (third) representative to either of the two states:

• Currently, the representative of state 1 represents 4000 people, while the representative for state 2 represents 16,000 people.  That’s a difference of 12,000 people per representative.
• If we give it to the first state, that state will have 2 representatives for 4000 people, so each representative will represent 2000 people.  This increases the disparity, to 14,000 people per representative.
• If we give it to the second state, that state will have 2 representatives for 16,000 people, so each representative will represent 8000 people.  This decreases the disparity, to 4000.

If our goal is to make the representation more nearly equal, we should give the third representative to the second state.  This is a “no brainer case”, because one assignment causes the disaprity to decrease and the other causes it to increase.

What about the next representative?

• Currently, the representative of state 1 represents 4000 people, while the representatives (two of them) for state 2 represents 8000 people, a difference of 4000 people.
• If we give the next representative to state 1, then the two representatives will represent 2000 people, increasing the difference to 6000.
• If we give the next representative to state 2, then the two representative will represent 5333 people (rounded), decreasing the difference.

Again, this is a “no brainer case”:  the second state should get the next representative.

The “no brainer” cases are easy to decide.  But what if neither of these are true?   If we follow the above, eventually we’ll get to a situation where the first state has 1 representative and the second state has 4.  However, if we’re apportioning 8 representatives, this means we still have representatives to assign.  So which state should get the next representative?  At this point, we have a problem:

• In both states, the representatives represent 4000 persons.
• Giving the extra representative to the first state means there will be 2000 persons per representative, increasing the disparity to 2000 persons.
• Giving the extra representative to the second state means there will be 3200 person per representative, which also increases the disparity (to 800 persons)

Here both assignments cause the disparity to increase.  Since we must assign a representative, we have to decide which state is more deserving even though this will increase the disparity.  Again, since our goal is to minimize the disparity, it should be clear that we want to choose the assignment that causes a smaller increase.   Thus, we’ll give the second state the next representative.

Continuing in this fashion, we can assign all eight representatives.  We’ll leave, as an exercise for the reader, the actual assignments.

With a little algebra, we can compute a formula that gives us the priority values for each state.  We can then solve the apportionment problem as above.

Unfortunately, we run into a problem. If we choose to minimize the difference between persons per representative, we get one rule for computing priority values. But if we choose to minimize the difference between representatives per person, we get a different rule. And if we choose to minimize the difference between the population and representative ratios, we get a third way to compute priority values.

One surprising way to get around this is to use the relative differences, expressed as a fraction of the smaller value.  I’ll leave off the math again (it’s not particularly difficult, but it is a little messy, and a blog isn’t the best medium…)

The punchline is this: all three relative differences are reduced by assigning the additional representative to the state with the higher priority value, when the priority values are computed by comparing 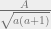 and .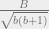

And this is exactly what we do, in the United States, to compute the number of representatives each state receives.

Of all the features of American-style democracy, this method of apportionment is a shining example of how democracies should be run.

Is Math White?

Unless you’ve been living under a rock, you’ll have heard about the allegations that math perpetuates “white privilege.”  My own take:  While there is some truth to the claim, we must be very careful about what conclusions we draw from them.

For example, part of the claim (nothing new, by the way…I heard the same argument back in the 1990s with the introduction of “multicultural mathematics”) is that names like “the Pythagorean theorem” perpetuate the idea that only white European men can do mathematics.  As a historian of mathematics, I know that “the Pythagorean theorem” was a) not actually discovered by Pythagoras, and b) was independently discovered by several cultures.  And it is my responsibility, as a historian, to set the record straight.

But what about my responsibility as a mathematician?  The issue is this:  when we teach the Pythagorean theorem as mathematicians, we don’t go out of our way to say “Pythagoras was a European white guy.”  What we usually do is to draw a triangle, label some sides, and say “Behold!  !”  (Yes, it is a reference…I can’t help myself)

Let’s contrast this to statues of confederate generals.  First, by the standard definition of treason (taking up arms against your country and losing), these folks were traitors, and a statue to Robert E. Lee is no more appropriate than a statue to Benedict Arnold or Nidal Hasan.

But legalistic issues aside, there’s a key difference. And that’s this:  What image pops into your head?  With “Robert E. Lee,” it’s the statue (or some other portrayal), and you know beyond a doubt that he was a European-descended white guy.  In contrast, with “Pythagorean theorem,” the immediate picture is that of a right triangle.

Math transcends nationality, culture, and gender.

But let’s take that a little further.  Part of the claim is that by emphasizing the importance of mathematics, we further disadvantage cultural groups that don’t, as a rule, do well in mathematics.  And that critique is valid…but what conclusion should we draw from it?

Should we conclude that we need to reduce the importance of mathematics?

Or should we instead conclude that it is more important than ever to make sure that all persons, regardless of gender, nationality, culture, sexual orientation, etc., have the opportunity for success in mathematics?

 

Flipped Classes: Improv and Scripted

I’m a great believer in flipped courses, and I’d like to say that everyone should teach this way.

But I won’t. There are some very real concerns about this type of instructional method. One hears horror stories about how instructors show videos to the class while they play a games on the computer, and I’m honest enough to say that I know it happens (for one thing, I’ve actually seen it happen). But I also believe that a bad teacher is a bad teacher regardless of the technology (and in fact, there is a long list of complaints about the teacher in question), so these reports should be viewed as indictments of the particular teacher and not the method.

But let’s say you’re a good and conscientious teacher who wants to do the best possible things for their students. The question you have to ask yourself is: Does a flipped class align with your personal teaching style?

Most mathematicians are gregarious extroverts who love going out and partying every night and meeting all sorts of new people and in general acting like Social Butterflies.

No, wait, those are reality TV contestants.

The stereotype is probably closer to the truth: most mathematicians are introverts with the social skills of a block of wood (or maybe MDF).   We take refuge in numbers, equations, and formulas because these allow for precision, unlike the fuzzy world of can you believe what he did or which of these two outfits look better.

The only time where this stereotype is broken is with teaching, because teaching is a social activity. So those of us who become teachers have managed to overcome whatever social anxieties we have and are able to get up in front of an audience and speak to them. In other words, we have learned to become performers.  We still have stage fright:  the difference is that we muscle through it.

Now comes the important part: there are two types of performers, which I’ll call the movie actor and the improv actor.  Neither type is inherently better; however, they rely on totally different skills, and you can be good at either or both.

A movie actor gets a fixed script and they work with it.  They’re distanced from their actual audience by time and space, and if necessary, they can do multiple takes to get things exactly right.

In contrast an improv actor has a script, but much of the performance relies on the interaction with the audience and at times the script may have to be dropped entirely because of the nature of the audience.

Movie actors are like those whose lecture; improv actors are like those who use flipped classes. If you like to maintain a comfortable distance between yourself and your students; if you take pride in an excellently organized presentation; if you like to fine-tune your examples and your jokes; then a straight lecture is probably better for your teaching style.

But if you like a more direct interaction with your students, where they can smell your halitosis or comment on your bald spot, and most importantly have to adjust instantly to what a student knows and doesn’t know to what they understand and don’t understand, then a flipped class might be better.

And that’s an important idea to keep in mind.  The two types of instruction require very different skills, and impose very different stresses.  The advantage of a lecture class is that you can prepare everything in advance, and barring the random chance of a fire drill or other emergency evacuation there are no surprises.  But if you’re teaching it flipped class you’re always living on the edge.

There are other things to consider if you want to do a flipped class. I’ll talk about that in a later post.

Math and Beethoven

You might have seen this problem making the rounds on social media:

First, the correct answer: it’s 40 minutes. Changing the size of the orchestra doesn’t change the time it takes to perform the symphony.  (Several people have noted, by the way, that this is a really fast rendition of the 9th symphony…Ode to Joy, as done by Alvin and the Chipmunks).

I’ve heard people say don’t need math to solve it; you only need “common sense.”   I despise that term:  “common sense” is invariably shorthand for “Don’t make me think about it.”  It’s “common sense” that there’s no point in educating women…at least, it was until about 200 years ago, when Mary Wollstonecraft  and others started questioning “common sense.” (And sadly, more than two hundred years later, you can find lots of places where the majority of the population still believes it’s a waste of time to educate women because, after all, it’s “common sense” that they’re just going to get married and have babies….)

Even worse, the “common sense” required for this problem (symphonies take the same amount of time to play regardless of how many people there are in the band) is only known to those familiar with symphonies and bands…and given the way we’re gutting the arts in education, that knowledge is less and less common.

These issues aside, this question is not only a legitimate math question, it’s actually a good one, because mathematics is more than filling in numbers and computing values.  What makes this a good question is that if you get the obvious wrong answer (80 minutes), you haven’t done mathematics:  you’ve just filled in numbers and computed values.  In particular, you’ve taken the formula that applies to

“If 2 eggs can make 6 brownies, then how many brownies can be made from 1 egg?”

and applied it to a different situation without asking the all-important question:  Is the reasoning from one problem applicable to a different problem?

This is the all-important question in mathematics, because mathematics is all about identifying the connections between different types of problems, with the goal of being able to solve a broad class of problems using a single approach.  (We even have a joke about it:  How many mathematicians does it take to screw in a light bulb?  One:  they give it to seven Lithuanians, reducing it to the previous joke)

It’s the all-important question in mathematics education, because problems in the real world don’t come with section labels.  You never know which approach will be useful on any given problem; you must constantly ask yourself is the reasoning from one problem applicable to another?

The formulas of mathematics are easy:  in fact, they are so utterly trivial that they can be programmed into a mindless automaton.  In an ideal educational system, the mindless automaton is an actual machine made of plastic and silicon.

The real work of mathematics has to be done by human beings.  An ideal educational system produces human beings who, as a matter of habit, ask the all-important question:  Does the reasoning applicable in one situation apply to this situation?

Lies Your Math Teacher Told You: PEMDAS

As most of us know, the basic operations of arithmetic are performed in a specific order. This is known as the order of operations, and is usually recalled by the mnemonic PEMDAS: parentheses; exponents; multiplication and division; addition and subtraction.  But even though we learn about PEMDAS in school, it’s important to understand that there are several falsehoods associated with it.

The first is rather subtle:  It’s that arithmetic operations must be done in this order.  This is true…except it isn’t.  In particular, while the order of operations is important, the actual order is less important than the fact that we agree on what the order should be.

The order of operations is a convention:  it’s an agreement on how we do things, but there’s no mathematical justification for it.  We don’t need to do multiplication before addition, any more than we need to drive on the right side of the road.  It’s certainly possible to drive on the left:

What’s important is not which side of the road we drive on, but that we agree which side of the road we drive on.  If some of us choose one side and some of us choose the other, then that’s a problem.

In fact, PEMDAS came about because  there was no general agreement on which side of the road we should drive on…I mean, because there was no standardization of the actual order.  It was only in the early years of the 20th century that the idea of a universal agreement on the order of operations came about (and a good thing, because soon after we were building electronic computers, and unless there was an agreement, a computer built in Britain might produce answers different from one built in the United States).

Another falsehood told about PEMDAS is that it’s PEMDAS.  It should actually be PEM/DA/S.

The MD in PEMDAS stands for multiplication and division. In PEMDAS, multiplication is listed before division, suggesting that in an expression like , you should multiply , then divide .

But in fact, multiplication and division are equiprecedent, meaning they are handled simultaneously. Again, this is a convention, like driving on the right side of the road.

This is unfortunately impossible, since one of them must be done first. But which one?

The answer is that we do them in the order they appear, from left to right.  In fact, the correct way to state the order of operations is:

All arithmetic operations are to be done from left to right, UNLESS…

Thus:  , since we take care of first, then multiply the result by .

There’s another problem with the way the order of operations is usually stated:  PEM/DA/S is better, but PM/DA/S is better still.

That’s because exponentiation isn’t an operation.

And here’s the lie that your math teacher told you:  You don’t do exponents before multiplication and division, because exponentiation isn’t an operation.

Exponentiation is a shorthand way of writing out a multiplication.  Remember that means .  Consider the expression:  .  Generations of students, having memorized PEMDAS, “do” the exponent first, and find .

But in fact, is not an operation:  it’s shorthand for .  In which case, .

Why does this matter?  There are several reasons.  First, if you try to find using PEMDAS and finding first, you’re stuck with the product .  On the other hand, if you recognize that is shorthand for “Multiply four 2s together,” then you have the much simpler task , where multiplying the 5 and 2 together gave us an easier product.

More importantly, consider scientific notation:  .  No one in their right mind wants to calculate (even though it’s not particularly difficult).  And they don’t have to:  scientific notation is shorthand.  In this case, is shorthand for the number we call one trillion, so is 8 trillion.  Likewise, shouldn’t be treated as the product of $5$ and whatever you get when you do the E in PEMDAS:    is shorthand for millionth and this number is 5 millionths.

The Mathematics of Medicare For All

Single payer is back in the political landscape (though, as even its supporters acknowledge, it has 0 chance of getting anywhere this cycle).  Let’s run the numbers.

First:  the US spends about $10,000 per person per year on health care.  If you follow the link, you’ll see that the actual value is different…but this is a math blog, so I’ll take it as a teachable moment of how to use estimates.

Second:  No one really knows how much MediCare for all would cost, but the most repeated estimate is around $1.5 trillion dollars.    Again, the link gives a slightly different number…

Third:  The US population is about 300 million.  

So divide one by the other, and you’ll find the MediCare for all would cost $5000 per person per year.  So one good argument in favor of such a plan is that most people, who buy their own insurance or who get insurance through their employer, pay more than this amount for their insurance, and when you add in the amount their employer chips in, you’re talking about an incredibly rare situation:  a government policy that benefits both employees (who take home more money) and their employers (who spend less on employee benefits).

Now here’s where the numbers get tricky.  If I’m a single person, then I win.  But what if I’m the sole wage earner supporting a family of four?  At $5000 per person, I’m now on the line for $20,000 in health insurance costs, which is far more than I would have paid.  Under these conditions, MediCare for all  is a losing proposition for me.

Here’s where things get complicated.  We’ll take an example from another context to see why:  If I’m a single person, then I spend about 10% of my income on food.  But if I’m the sole wage earner supporting a family of four, the amount I spend on food will not be 40%.  Instead:

• If my single income can support a family of 4 in the same lifestyle that it supports a single person, then my food outlay is still going to be around 10%.
• On the other hand, if my single income can only support one person, then that food budget will expand significantly.

A better way to look at it is through the federal budget (since it will, sooner or later, be paid for by taxes).  Currently, MediCare runs around $500 billion, so MediCare for all would add $1 trillion to the federal budget.  The federal budget itself is around $4 trillion, so we’re talking a 25% increase in the federal budget.  

There’s many ways to pay for this, but the simplest is an across-the-board increase in taxes by 25%.  (Sanders plan incorporates a variety of methods to reduce the “average” pain, but that would complicate the analysis below…I’m not a policy wonk)

Now before you reach for your phone (email, pen and paper) to write your Congresscritter, let’s put this 25% increase in perspective.  Remember that MediCare for all would replace what you’ve spent on health insurance.  So the key equation is

If your current health insurance is more than a 25% tax increase would be, you’ve won. Otherwise, you lose.  To determine this, multiply by four:

This gives you a gauge of whether you win or lose under MediCare for all:

• Take the amount you spend on health insurance.   Multiply it by 4.  If the amount is greater than your taxes, then you win.
• Otherwise, you lose.

If you’re making $100,000 a year, you’re probably paying about $20,000 in federal taxes (unless you have a really, really bad accountant…or a really, really good one).  This means that if you’re paying more than $5000 a year in health insurance, you win under MediCare for all.  

God and Probability

In 1710, John Arbuthnot, an English physician, published an article proving the existence of God.  Arbuthnot’s argument was based on the following:

• For 82 years, the number of boys born in London has been greater than the number of girls born in London.
• This is too unlikely to happen by chance.  Therefore, “Divine Providence” arranged it.

To see why this argument isn’t a good one, consider the analogous argument: I have a rock. When I let it go, it can either fall up or fall down. So if I let it go 100 times, the chance of it falling every time is in , which is so small that we may regard this occurrence as impossible.

And yet, the rock falls every time. Does this improbable event prove the existence of “not a sparrow falls” God?

This example should make clear the flaw in Arbuthnot’s argument, as well as those of his modern emulators. The probability assumptions being made are questionable. Arbuthnot assumed boys and girls were born with equal frequency, and when he found they weren’t, concluded God exists. But a better conclusion is that boys and girls aren’t born with equal frequency… because the evidence says they’re not.

This leads to the following conclusion: no probability argument can be used to prove the existence of God. This is because the underlying probabilities are always subject to debate.

For example, if I flip a coin and it lands heads 99 times in a row, I could believe I’ve just witnessed an extremely improbable event. But I’m more inclined to conclude the coin isn’t a fair coin.

Or say we find intelligent alien life out there, a la Star Trek, with one difference: every species we encounter is genetically identical to modern humans. Would this be evidence for a God who made man in His image?

I’ll admit, I’d wonder. But ultimately, I’d question the assumption that the human form is the product of random selection in the genetic lottery: Maybe there are undiscovered laws of physics that favor five phalanged bipeds without feathers. (Science fiction offers other scenarios, e.g. alien gardeners who make species in the form they want, and if you choose to believe God is an alien gardener, then this is an argument that would be compelling)

Flip Your Class! (Or not)

There’s been some buzz about a new style of teaching called a flipped or inverted class. The proponents make grand claims about how it will revolutionize education. Of course, we’ve heard these claims before, so we’re inclined to be a little hesitant.

Before addressing these claims, let’s consider what the flipped class replaces. In a traditional math class, students go to class to hear a lecture, then go home to do an assignment.

Let’s consider a good, conscientious student. Even if they do the work, the earliest they’ll get feedback on whether they’ve done it correctly is two days after they were exposed to the material: If the lesson was taught on Monday and the homework turned in Tuesday, they won’t get it back until Wednesday. That means that if they didn’t understand the material, they are now two days into new material. This is a common problem in math: If you get behind, you stay behind.

So how can we solve this problem? The best way is to have the student working a problem under guidance, with constant feedback. That way, any misunderstandings or misconceptions can be cleared up before the student moves on to the next section.

The ideal situation is to have the teacher give a lecture, then work with the students to solve problems. That works well…as long as the lecture is short enough to allow time to solve problems. Some of the classes I teach are 3 hours and 45 minutes, and I can lecture and work with students.

The problem is that with shorter classes you have to choose: lecture or student work? The problem gets magnified when you have to “cover” material and complete a set list of topics in a semester.

The solution offered by a flipped class is to move the lecture offline…by putting it online. Then all of class can be spent on student work. This is the heart and soul of a flipped class: students sit through the lecture at home, then do assignments in class with guidance and supervision.

First, let me extol the advantages. There are many:

• Taking notes in mathematics is like writing down the score of a symphony. Even if you capture everything perfectly, you will still miss the nuances, because math is a process, not a product. Ever try to learn woodworking by reading a book? I have…and amazingly enough, I can still count to 9 and 1/2. But I fixed the belt on our dryer by watching the repair guys on YouTube.
• Lectures proceed at the pace of the instructor. But that will almost always be too fast for some students and simultaneously too slow for others. Videos can be played at half speed or double time. And if you miss something, there’s always rewind.
• A good lecture tries to get audience engagement by asking for input: “So what’s the next step?” The problem is either that no one knows, so there’s along, awkward pause before the lecture continues, or someone does and gives the answer. While the latter is a good thing, in practice only a few students have the opportunity to answer, and the students who might be able to answer, but take a little longer to get there, lose the chance to contribute. But they can hit pause and take as long as they need to collect their thoughts.

Now if you read the foregoing carefully, you’ll realize that, while these are arguments for using math videos, they aren’t necessarily arguments for flipped classes.

And that’s because flipped classes aren’t for everyone. I’ll talk about that in a later post.